0 前言
隨著制造業的不斷發展,復雜型面工件加工的用戶需求日益擴大,因此,對復雜曲線運動規劃方法的研究,也日益成為數控技術發展的首要任務,是否具有復雜曲面的加工功能,已成為評價高性能數控系統的重要指標之一。
1 開放式數控系統樣條曲線運動規劃概述
采用直線插補,實現對復雜曲面的高速、高精度加工需要較高的配置。除了通過用直線段逼近復雜曲線來實現對復雜曲面的加工外,還可以用樣條來擬合復雜曲線,通過直接對樣條曲線進行插補來實現對復雜曲線的加工。在相同精度的條件下樣條曲線比直線段能描述更長的零件輪廓,首先,對于同一個復雜曲面來說,在相同的精度條件下,用樣條擬合后,其G代碼文件的大小不會超過用微小直線段方法的1/10;其次,由于在相同精度的條件下樣條曲線段比直線段能描述更長的零件輪廓,因此,采用樣條方法后,每條G代碼規定的刀具路徑的長度遠遠大于用微小直線段方法的刀具路徑長度,這樣解釋器在單位時間內可以解釋更長的刀具路徑,使原來的數據饑荒問題可以得到解決。另外由于樣條曲線可達到C2連續光滑,能夠避免刀具運動方向的突然變化,并能改善刀具的受力情況,使得刀具可以光滑地、“柔順地”從一點移到另一點,不會出現任何突然轉向,從而可以提高加工精度。由此看出,采用樣條方法可以以較小的成本,實現對復雜曲線的高速、高精度加工。由于樣條方法具有G代碼文件小、擬合精度高、進給速度大、無數據饑荒等優點,樣條插補已經逐漸應用于高檔NC系統。采用參數樣條曲線的優點表現為所有有關曲線的操作都是在參數域內進行的,如各坐標點的計算,曲線的幾何變換等,而且參數曲線的坐標維數可以方便地增加,數控插補中的多坐標聯動插補可以直觀地通過參數聯系起來。需要解決的關鍵問題是三次樣條長度的計算、步長參數的計算、插補遞推公式、以及根據步長參數求得三次樣條曲線上對應的型值點。
2 刀具軌跡曲線的描述
三次樣條曲線可以用下列參數方程表示:
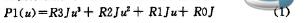
式中:RK,J(K=1,2,3)是第i段三次樣條的系數矢量矢量,可以是二維的,也可以是三維的;u是無量綱參數,其取值范圍為:0≤u≤1。
由上式可知,如果給定n+1個節點坐標和2個邊界條件,就可唯一確定一條刀具軌跡曲線,即通過求解所構成的n+l維線性方程組,可以得到通過任意兩個相鄰節點Pl和Pl+1,的三次樣條曲線段的多項式矢量系數RK,Jk(k=1,2,3)。
在采用基于S曲線加減速的運動規劃方法時,需要注意的是如何從三次樣條曲線上得到輪廓步長為ds時對應的軌跡點,以及三次樣條曲線的長度計算。
3 步長參數的計算及插補遞推公式
步長參數的計算必須保證算法能在一個插補周期內實時完成,因而算法應盡量簡單。由于每個步長參數增量都是對應于一個插補周期的,因而弦長相對于整個曲線而言是一個小量,為簡化計算可用弧長ds代替弦長,由式(1)可得:

到此為止,可以按如下方法計算步長參數u,根據u計算得到三次樣條曲線上的型值點:在插補開始時,u0=0,由此可以得到插補遞推公式:
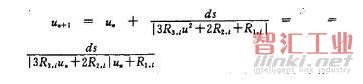
參數u確定以后,根據式(1)可以很容易得到每個第n個插補周期的型值點。4 三次參數樣條運動規劃方法的實現
在參數三次樣條運動規劃方法的實現中定義了如下C結構體來描述兩個型值點之間的三次樣條曲線:

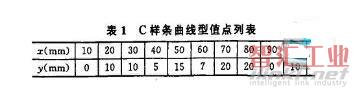
由于在三次樣條曲線的構造過程中,要求解,t+1維線性方程組來確定各段三次樣條的系數,這個過程中包含大量的浮點運算,使算法的實時性難以得到保證。因此,在三次樣條曲線運動規劃方法實現中,應該引入了一個三次樣條運動規劃預處理指令,通過該指令,把計算量較大、實時性要求不高的工作,如計算出各軸的三次曲線參數方程的系數及三次樣條的長度等放在預處理階段完成。當預處理結束時,才開始三次樣條曲線的實時插補,參數化三次樣條實時插補算法流程如圖1。在非實時仿真環境下對表1給出的型值點對應的C樣條曲線進行了規劃測試,參數配置如下:amax=1000m/s2;v=150mm/min;vmax=6000mm/min;cycleTime=0.002s。其中,amax為最大加速度,、為指定的編程速度,vmax系統的軸最大速度,cycleTime為插補周期。
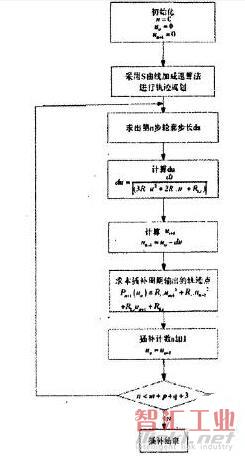
圖1 三次樣條實時插補算法流程
由測試可知(曲線圖略,可以根據值點列表對應得出),基于樣條曲線的運動規劃方法也可以在數控的運動控制器中實現。
(審核編輯: 智匯張瑜)
分享