0 引言

　　目前，仿真技術往往被用于在設計之后進行模擬試驗，其實也可用于復雜系統的設計求解。采用PID控制的控制器設計，為兼顧快速性和穩定性，其控制參數較難確定，而且依靠軟硬件實現都比較麻煩。由于進給伺服系統趨于數字化，即控制方法采用時間離散型采樣控制，控制器可采用差分模型，先找出系統輸入輸出的一些關系，再用仿真的方法來反求控制器的各系數，這也是一種有效的設計方法。

1 控制器數學模型的建立

　　建立控制器數學模型，PID控制器的傳遞函數為:

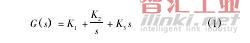
　　PID控制器的框圖見圖1。

　　上述公式是線性常系數差分方程組，以此作為控制器的數學模型方便計算機控制系統的實現。差分方程控制器D(Z)模型見圖2。

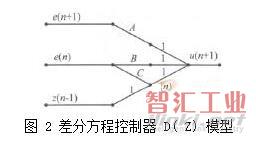
2 伺服驅動系統數學模型的建立

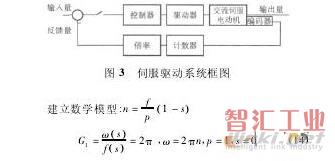
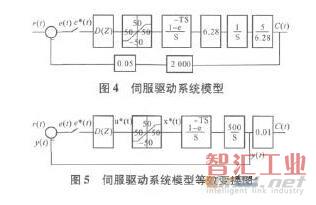
　　根據數控木工加工中心進給速度要求高，而加工精度要求相對低一點的特點，采用半閉環伺服系統和數字控制方式。將伺服進給系統分成機械傳動機構和伺服驅動系統。設計要求為進給速度為15m/min，脈沖當量為0.01mm。選擇電動機:MDDDT5540，額定功率為1kW，最高轉速為3000r/min，增量編碼器為10000p/r，絲杠螺距為5mm。為簡化結構，只設位置環，不設速度環。伺服驅動系統框圖見圖3。

　　交流伺服電動機，增量編碼器G2=10000P/5mm=2000P/mm，倍率G4=1/(2000×0.01)=0.05。驅動器:一部分為零階保持器，一部分為限幅器，計數器G3=1。控制器:D(Z)。伺服驅動系統模型見圖4，等效變換見圖5。

3 伺服驅動系統仿真設計

　　加入非線性環節的系統進行仿真的方法:分別求取差分方程控制器的差分方程與連續部分的脈沖傳遞函數的差分方程，在每一個響應時刻分別對兩部分進行一次計算，插入非線性環節，連接輸入輸出，以得到控制器下一時刻的輸入。控制器差分方程:

　　飽和非線性環節:當u(n)≥50時，x(n)=50;當－50≤u(n)≤50時，x(n)=u(n);當u(n)≤－50時，x(n)=－50。連接方程:e(n)=r(n－1)－y(n－1)。如果仿真也像神經網絡法一樣去進行訓練是行不通的，一是太多的樣本難以獲得，二是計算量太大。其實只要找出系統的輸入輸出在趨于穩定狀態時的關系，仿真求出滿足關系的一組控制器方程組系數即可。根據系統的穩定性、快速性、準確性要求確定輸出響應。伺服驅動系統在v=15m/min，脈沖當量為0.01mm，y(t)=1時，穩態時間應在4×10－5之內。時間在0～10－6s，系統加速;時間在10－6～3.5×10－5s，系統勻速，以最高速度運動;時間在3.5×10－5s～3.6×10－5s，系統減速;時間在3.6×10－5s～4.0×10－5s，系統趨于穩定并達到穩態值。系統希望的單位階躍時間響應曲線見圖6，

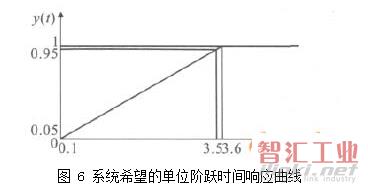
　　伺服驅動系統輸入最高頻率為25000Hz，反饋最高頻率為50000Hz，根據采樣定理，取采樣頻率為106Hz，采樣周期T=10－6s。當r(t)=1時，控制y(35)，y(36)，y(37)和y(38)等的值，通過仿真反求出一組滿足條件的系數ABC。仿真程序框圖見圖7。

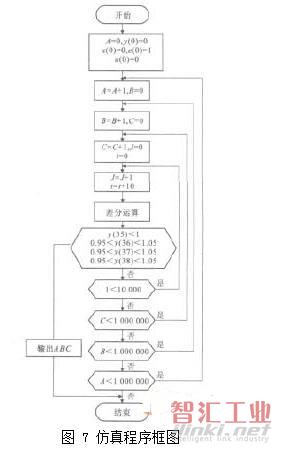
　　仿真結果:A=431500，B=25200和C=500，將求得的ABC值帶入數學模型，再次仿真，取T=10－6s，n=100，求解得輸出響應見圖8。仿真結果:調整時間為4.0×10－5s，輸出誤差在±0.05之內。換算成進給速度為15m/min，正好達到設計要求。

4 結論

　　伺服驅動系統控制器的設計采用差分方程組作模型簡單可行，只要將控制器的設計和系統的設計融為一體，建立各部分的差分模型，找出系統輸入輸出在趨于穩定狀態時的關系，仿真求出滿足關系的一組控制器差分方程組系數即可，而該模型又方便在數字伺服驅動系統中靠軟件實現。